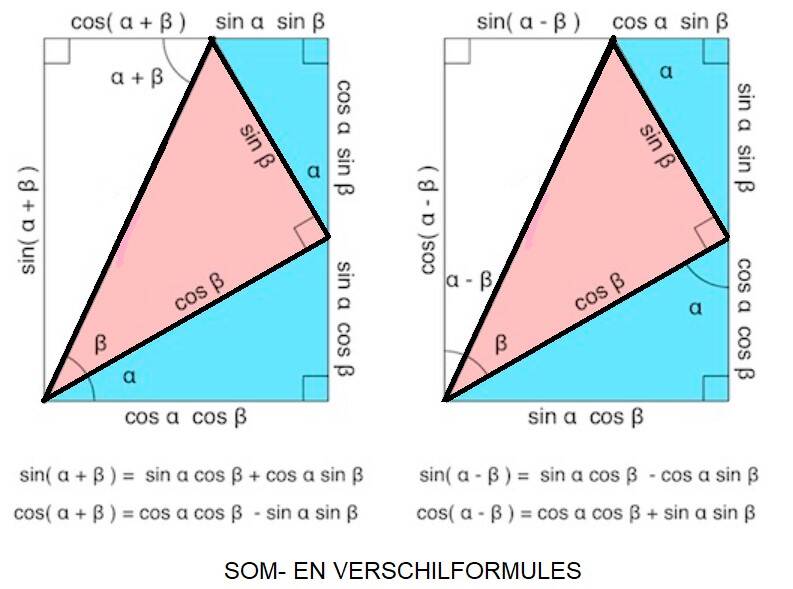
Hieronder kan je even meegenieten van een reeks 'Griekse bewijzen'.
Wat wij nu vaak langs algebraïsche weg (met formules) bewijzen,
werd oorspronkelijk via meetkundige figuren aangetoond.
Onder het motto 'WISKUNDE ZIE JE!' , kan je hier dus enkele bewijzen zo maar op de figuur aflezen.
De eerste figuur toont op de typisch Griekse manier, d.w.z. via een meetkundige figuur aan
dat de 'oneindige som' 1/2 + 1/4 + 1+8 + 1/16 + 1/32 + ... gelijk is aan 1.
Het vierkant met oppervlakte 1 wordt immers opgevuld met vierhoeken
waarvan de oppervlakte gelijk is aan 1/2, 1/4, 1/8, 1/16 , ... enz.

Hieronder staan nog drie figuren waarmee men kan aantonen dat de 'oneindige som'
1/4 + 1+1/16 + 1/64 + ... (waarin elke volgende breuk vier keer kleiner is dan de vorige) gelijk is aan 1/3.
Zie je het bewijs?



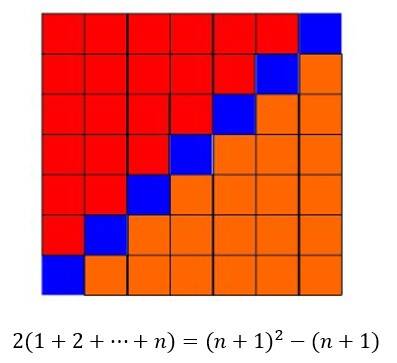
Hieronder staat een bewijs zonder woorden voor de somformule 1 + 2 + 3 + ... + n = n(n + 1)/2.

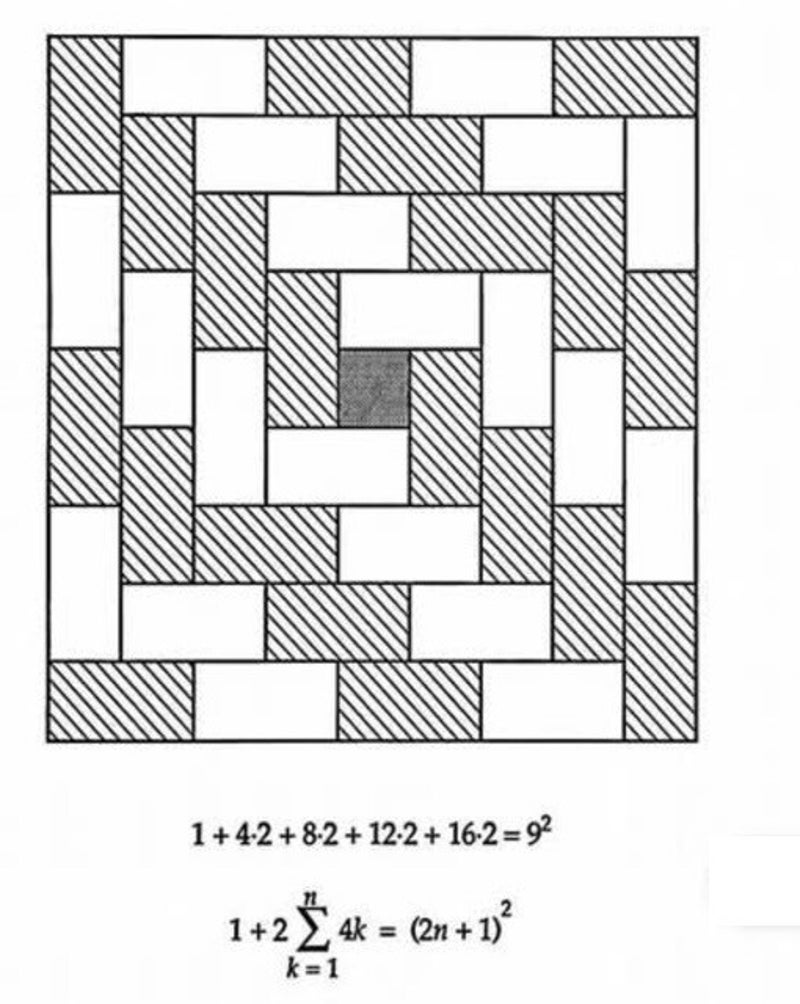
En hieronder zie je waarom 1 + 3 + 5 + ... + (2n – 1) = n².

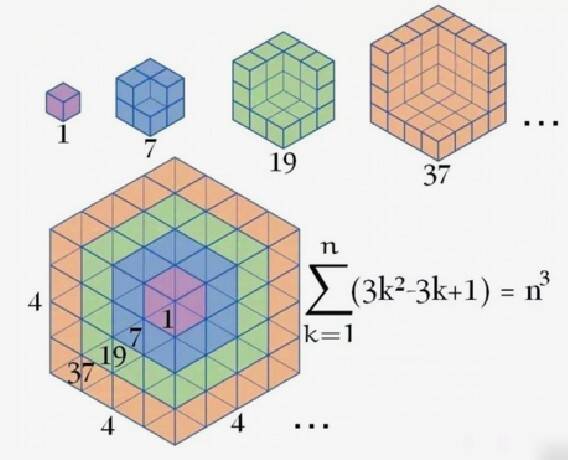
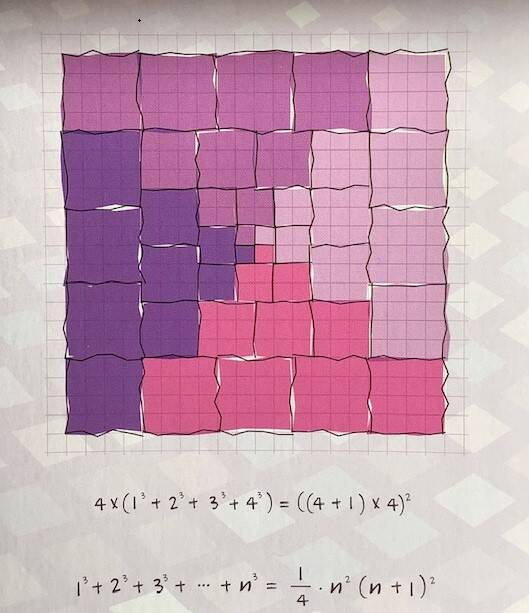
Wist je dat 1³ + 2³ + 3³ + 4³ = (1 + 2 + 3 + 4 )² (en dat kan je veralgemenen) ?
Hierbij werd gebruik gemaakt van het feit dat 2 × 2² = 2³ en 3 × 3² = 3³ en 4 × 4² = 4³.













4/9 + 4/81 + 4 /324 + ... = 1/2

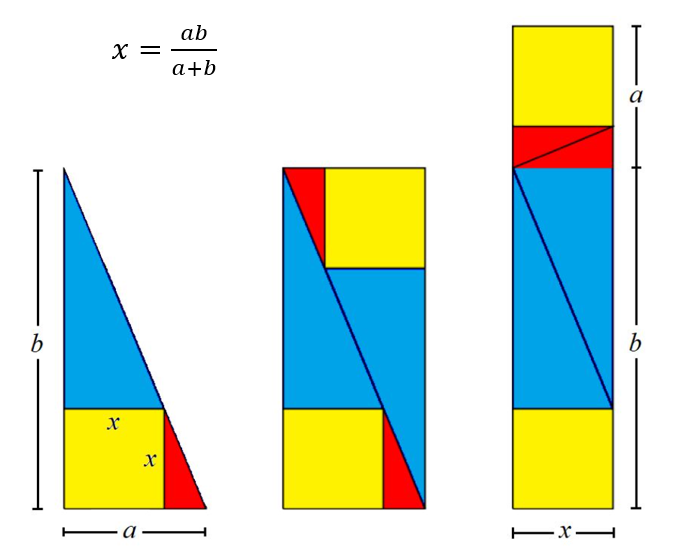
Mijn bewijs voor een gekende formule.


a² - b² = (a + b)(a - b)









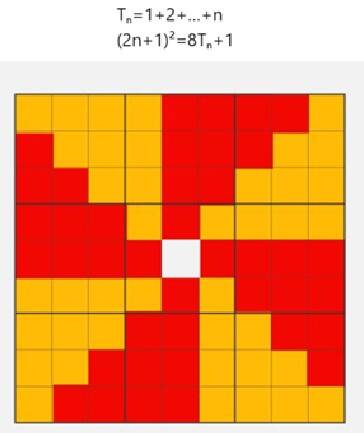
UITLEG BIJ DE BOVENSTAANDE FIGUUR.
Links staat in elke driehoek (dus 3 keer) de som 1² + 2 x 2 + 3 x 3 + ... + n x n = 1² + 2² + 3² + ... + n².
Getallen in die deze driehoeken op dezelfde plaats samengeteld geeft telkens 2n + 1.
In de rechtse driehoek staat bijgevolg n(n + 1)/2 keer 2n + 1.











Bron: tijdschrift Pythagoras
____________________________________________


_________________________________________________________________________















Deze tekst past bij de figuur hiernaast.
De voorwaarde is dat a² + b² = c², d.w.z. dat a, b en c de lengtes zijn
van de zijden van een rechthoekige driehoek.

TWEE FORMULES VOOR DE STRAAL VAN DE INGESCHREVEN CIRKEL VAN EEN RECHTHOEKIGE DRIEHOEK












In het magazine KNACK van 19 april 2000 publiceerde Gerard Bodifée
een opmerkelijke column met een veelzeggende titel.
Daarin verdedigt hij met klem 'de zuivere wiskunde'.
Moet je beslist eens lezen!

Hieronder vind je een document met 12 bewijzen zonder woorden
en een opdracht om elke figuur te koppelen aan de corresponderende eigenschap of stelling.
Maak jouw eigen website met JouwWeb